本記事では畳み込み積分について説明します.
基本的には連続な関数に対しての畳み込みを説明しますが, 離散な関数に対しての畳み込みも同様の考え方で大丈夫でしょう.
読み物感覚で見てもらって間違いとかあったらぜひ指摘ください.

前提知識

基本的に本記事では理論的な話をふんわりとした感じで書くので 積分を区分求積法のイメージで理解できればだいたい理解できると思います。

対象読者

畳み込み積分をはじめてきいた人
授業で習ったけどよくわからない人

フィルタ処理によるノイズ除去

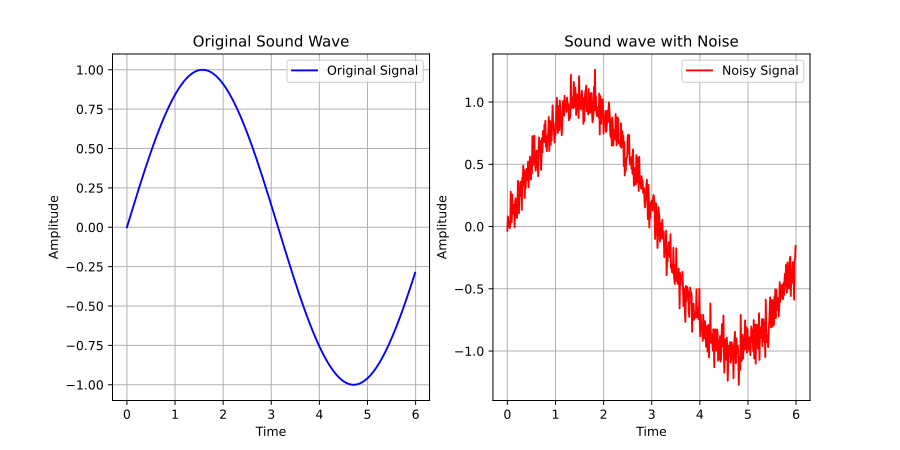
音声信号を例にとってみます. 一般に音声をグラフに示すときには横軸に時間$t$を, 縦軸に振幅$x(t)$をとります. 上の図をご覧いただきたい. 左側には私の声を示すグラフがあります. きれいな正弦波ですね.
しかし, 一般に録音を行うとどうしても環境音などの細かなノイズが入ってきてしまいます. そうすると, 右のグラフのようにノイズが乗っかかってきて ギザギザなグラフになってしまいます.
どうにかしてこのノイズを取り除いて, 左側の真の私の声を取り出す方法はないだろうか.
賢いsさんは考えました.

ノイズの平均はゼロとなるはずだから, 振幅を知りたい音声の時間を$t'$としたときに, $t'$の前後一秒間の振幅の平均をとれば ノイズは打ち消しあって, 音声の振幅が得られるのではないか.

連続関数$x(t)$に対して, $t'$の前後一秒間の振幅の平均をとるというのは, 式に直せば $$ \frac{1}{2} \int_{-1}^{+1} x(t' + t) dt $$ となります.
つまり, $x(t)$の$[t'-1, t'+1]$の区間の合計$\int_{-1}^{+1} x(t' + t) dt$を区間の長さ$2$で割ったものです.
実際にこの処理をかけてみると, 
のようになります.
確かにグラフのギザギザはなくなりました. しかし, オリジナルの音声のグラフの振幅の絶対値の最大値は1.0であったのに対して, こちらは0.75程度となっています.
これではオリジナルの音声を復元できたとは言えないでしょう.
sさんはこの誤差の原因についてこのように考えました.

ノイズの関数をn(t)とし, オリジナルの音声の関数をx(t)としたときに, 録音された音声の関数はx(t) + n(t)となる.
単純に平均をとっただけではn(t)が平均されて0になるだけでなく, x(t)も平均されてしまうではないか.
しかし, 録音された音声のn(t)だけを取り出すことはできない.
ならばせめて影響を小さくするために, 前後一秒間ではなく, 前後0.1秒間の平均をとるのはどうだろうか.

このとき, ノイズ除去された音声の関数は $$ \frac{1}{0.2} \int_{-0.1}^{+0.1} x(t' + t) dt $$ となります.
これの処理をかけた結果は 
となります.
最大値はたしかに1.0程度となりましたが, グラフががくがくしていて正弦波には見えません.
sさんの苦戦を見ていたgさんはこのように言いました.

フィルタをかける時間区間を変えてもうまくいくかもしれないけど,
いい感じの時間区間を見つけるためには何度も実験して確認しないといけないよね.
データが違えばそのデータにあった時間区間を実験で見つけないといけないなんてめんどくさすぎる.
私なら時間は前後一秒間に固定して, フィルタを変えてみるかな.
例えば, フィルタの中央の値の影響を大きくして, その周りの値の影響を小さくするフィルタなんてどうかな.

そんなことを言いながら, gさんは $$ \frac{3}{\sqrt{2\pi}} e^{-\frac{9t^2}{2}} $$ を持ち出してみました.
この関数でフィルタを行うと, $$ \int_{-1}^{+1} x(t' + t) \frac{3}{\sqrt{2\pi}} e^{-\frac{9(t)^2}{2}} dt $$というようになります.
このグラフの概形は下図のようになります. 
グラフの$[-1, 1]$の区間の外ではほとんど関数の値は0に近い値になっています. 実際, このグラフの$[-1, 1]$の範囲を積分してみると 0.9973程度になります.
この関数で処理してみると,  のようになります.
単に平均値をとる処理よりかはきれいですね.

フィルタの一般化

このように, 信号$f(t)$に対しては, 用途や必要な精度に応じて, フィルタの関数や適用区間を変えることがあります.
どのようなフィルタや時間区間にも適用できるように, フィルタ処理を一般化すると$$ filtered(t') = \int\limits_{S} f(t' + t) h(t) dt $$となります.
ただし, $S$というのは実数上の区間で, 特に$[-1, 1]$である必要はなく, 例えばフィルタの特性や, リアルタイム処理で未来のデータが得られない場合には$[-1, 0]$のようなフィルタを用いることもあるでしょう.
ここで, $$ \tilde{f}_S(t) = \begin{cases} f(t) & (t \in S) \\ 0 & (t \notin S) \end{cases} $$ $$ \underline{h}(x) = h(-x) $$ という新たな記法を導入します. 一般的な数学の記号ではありませんので他のところでは使わないほうがいいです.
この一般化されたフィルタをさらに変形してみましょう.
$$ \begin{align*} filtered(t') &= \int\limits_{S} f(t' + t) h(t) dt \\ &= -\int\limits_{-S} f(t' - t) h(-t) dt \\ &= -\int\limits_{-S} f(t' - t) \underline{h}(t)dt \\ &= -\int_{-\infty}^{\infty} \tilde{f}_S(t' - t) \underline{h}(t) dt \\ &= -(\tilde{f}_S * \underline{h})(t') \end{align*} $$ なじみのある畳み込みの形になりました.
ここで, $\tilde{f}_S$は単に信号を0でパディングした関数, $\underline{h}$はフィルタの関数を反転させたものなので, 畳み込みの正体というのはフィルタ処理といえるでしょう.

周波数領域での話

ノイズとは何でしょう. 再び最初の図の右のグラフを見てみましょう. とてもギザギザですよね.
ギザギザというのはすなわち, 値の変動が激しい高周波数成分が含まれているということです.
このノイズが含まれたギザギザのグラフにフィルタ処理を行うと, なめらかなグラフになります.
なめらかというのは値の変動が少ない低周波数成分の影響が強いということです.
つまり, 私たちが今までやってきたフィルタ処理というのは高周波数成分を除去して, 低周波数成分を強調する処理を行っているということです.
このような効果をもたらすフィルタをローパスフィルタと呼びます.
ただし, フィルタの中には高周波数成分を強調するフィルタもあります.
例えば, 画像処理でエッジを強調するフィルタなどは高周波数成分を強調するフィルタです.
このようなフィルタをハイパスフィルタと呼びます.
周波数の話をするならフーリエ変換$$ \mathcal{F}(f(t)) = F(\omega) = \int_{-\infty}^{\infty} f(t) e^{-i\omega t} dt $$は通れないでしょう.
$F(\omega)$は一般に複素数となり, 信号に含まれる$a sin(\omega t + \phi)$のような成分の様々な情報を表します.
$F(\omega)$の虚部は成分の位相を表し, 実部は成分の振幅を表します.
フーリエ変換を畳み込み積分に適用すると, $$ \mathcal{F}(f(t) * g(t)) = \mathcal{F}(f(t)) \cdot \mathcal{F}(g(t)) $$となります. つまり, 畳み込みによってフィルタをかけているとき, 周波数領域でもフィルタをかけているのです.
証明は教科書に書いてあると思います.

高次元での話

ここまで説明してきた話は高次元でも成り立ちます.
フーリエ変換と畳み込み積分の関係の証明は一次元のときと同様に積分の順序交換を行えばいいと思います.
まあ現実的にはせいぜい三次元動画像の属する四次元くらいまでじゃないんですかね使うことがあるとしても.